文章地址：A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise

DBSCAN(Density-Based Spatial Clustering of Applications with Noise)，具有噪声的基于密度的聚类方法，是一种很典型的密度聚类算法，他和K-Means，这种一般只适用于凸样本集的聚类相比，DBSCAN 既可以适用于凸样本集，也可以适用于非凸样本集。

密度聚类的原理

• DBSCAN 是一种基于密度的聚类算法，这类密度聚类算法一般假定类别可以通过样本分布的紧密程度决定。
• 通过将紧密相连的样本划为一类，这样就得到了一个聚类类别。
• 通过将所有各组紧密相连的样本划为各个不同的类别，则我们就得到了最终的所有聚类类别结果。

DBSCAN 中关键的几个定义

假设样本集D=(x1,x2,...,xm)，参数(Eps, MinPts) 用来描述邻域的样本分布紧密程度。

其中，Eps描述了某一样本的邻域距离阈值，MinPts描述了某一样本的距离为Eps的邻域中样本个数的阈值。DBSCAN 具体的密度描述定义如下：

1. core point 核心节点： 在距离节点 p Eps内（包括p）如果至少有minPts个节点，那么节点p是核心节点。
2. directly density-reachable 直接密度可达： 如果节点 q 与核心节点 p 的距离在Eps范围内，则节点 q 可以从 p 直接到达。点仅被称为可以从核心点直接到达。
3. density-reachable 密度可达： 如果存在路径p1，...，pn（p1 = p和pn = q），则从 p 可以到达点 q，其中每个pi + 1都可以直接从 pi 到达。 注意，这意味着初始点和路径上的所有点都必须是核心点，q 可能例外。
4. noise points or outliers 噪声点或离群点： 从其他任何点无法到达的所有点都是离群点或噪声点。

图中：A、C直接密度可达；B、C密度可达、N 为离群点

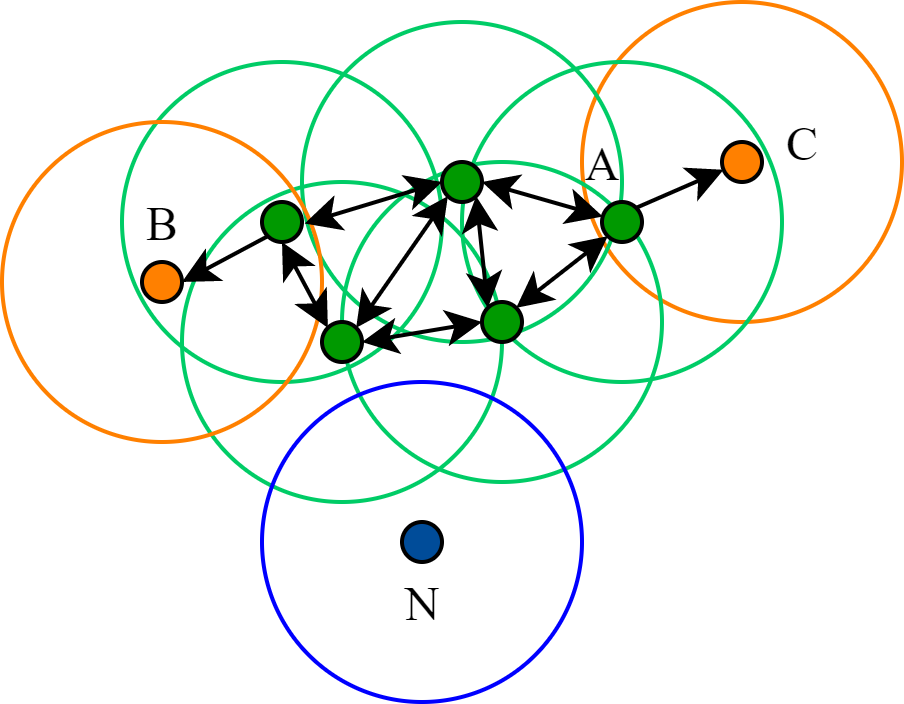
DBSCAN 的聚类思想

1. 由密度可达关系导出的最大密度相连的样本集合，即为我们最终聚类的一个类别，或者说一个簇。
2. 这个 DBSCAN 的簇里面可以有一个或者多个核心对象。
   1. 如果只有一个核心对象，则簇里其他的非核心对象样本都在这个核心对象的ϵ-邻域里；
   2. 如果有多个核心对象，则簇里的任意一个核心对象的Eps-邻域中一定有一个其他的核心对象，否则这两个核心对象无法密度可达。
   3. 这些核心对象的Eps-邻域里所有的样本的集合组成的一个DBSCAN聚类簇。

那么怎么才能找到这样的簇样本集合呢？

DBSCAN 任意选择一个没有类别的核心对象作为种子，然后找到所有这个核心对象能够密度可达的样本集合，即为一个聚类簇。

接着继续选择另一个没有类别的核心对象去寻找密度可达的样本集合，这样就得到另一个聚类簇。一直运行到所有核心对象都有类别为止。

这里有一个问题没有考虑：

对于某些样本可能到两个核心对象的距离都小于Eps，但是这两个核心对象由于不是密度直达，又不属于同一个聚类簇，那么如果界定这个样本的类别呢？

一般来说，此时 DBSCAN 采用先来后到，先进行聚类的类别簇会标记这个样本为它的类别。

这也是导致 DBSCAN 的算法结果不稳定的原因之一。

小结

• 优点
  1. 和传统的 K-Means 算法相比，DBSCAN最大的不同就是不需要输入类别数k，当然它最大的优势是可以发现任意形状的聚类簇，而不是像K-Means，一般仅仅使用于凸的样本集聚类。
  2. DBSCAN具有噪声概念，并且对离群点具有鲁棒性。
• 缺点
  1. DBSCAN 的算法结果取决于在函数 regionQuery（P，Eps）中使用的距离度量。 最常用的距离度量是欧几里得距离。 尤其是对于高维数据，由于所谓的“维数诅咒”，该度量几乎变得无用，从而很难找到合适的ε值。 当然，这种效果在基于欧几里得距离的任何其他算法中也存在。
  2. 对于密度不均匀的数据集不能很好的进行聚类，因为不能选择出合适的参数（Eps，minPts） End.